Распределения дискретных случайных величинБиномиальное распределение. Дискретная случайная величина Х имеет биномиальное распределение , если ее возможные значения 0, 1, 2, ... , m , … , n , а соответствующие им вероятности равны:
где 0 <
p
< 1,
q
= 1 –
p
;
m
= 0, 1, 2, ... ,
n
.
Как видно из (21), вероятности
Р
m
вычисляются, как члены разложения бинома Ньютона
Примером является выборочный контроль качества производственных изделий, при котором отбор изделий для пробы производится по схеме случайной
повторной выборки
, т.е. когда проверенные изделия возвращаются в исходную партию. Тогда количество нестандартных изделий среди отобранных есть случайная величина с биномиальным законом распределения вероятностей.
Биномиальное распределение определяется двумя параметрами: n и p . Cлучайная величина, распределенная по биномиальному закону, имеет следующие основные числовые характеристики:
Распределение Пуассона. Дискретная случайная величина Х имеет распределение Пуассона , если она имеет бесконечное счетное множество возможных значений 0, 1, 2, ... , m , …, а соответствующие им вероятности определяются формулой:
Примерами случайных явлений, подчиненных закону распределения Пуассона, являются: последовательность радиоактивного распада частиц, последовательность отказов при работе сложной компьютерной системы, поток заявок на телефонной станции и многие другие.
где 0 < p < 1, q = 1 – p ; m = 0, 1, 2, ... .
Вероятности
Р
m
для последовательных значений
m
образуют геометрическую прогрессию с первым членом
р
и знаменателем
q
, откуда и название «геометрическое распределение».
В качестве примера рассмотрим стрельбу по некоторой цели
до первого попадания
, причем вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов и сохраняет постоянное значение
р
(0 <
p
< 1). Тогда количество произведенных выстрелов будет случайной величиной с геометрическим распределением вероятностей.
Геометрическое распределение определяется одним параметром р . Cлучайная величина, подчиненная геометрическому закону распределения, имеет следующие основные числовые характеристики:
Гипергеометрическое распределение. Дискретная случайная величина Х имеет гипергеометрическое распределение с параметрами a , b , n , если ее возможные значения 0, 1, 2, ... , m , … , а имеют вероятности:
|
Содержание
>> Прикладная математика
>> Математическая статистика
>> Элементы математической статистики
>> Распределения дискретных случайных величин
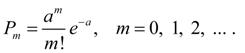 (23)
(23)
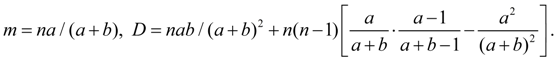 (28)
(28)