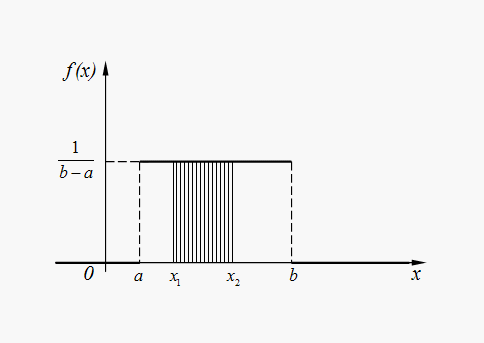
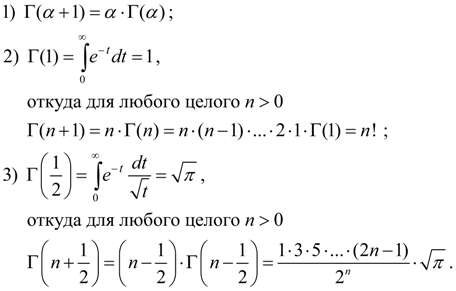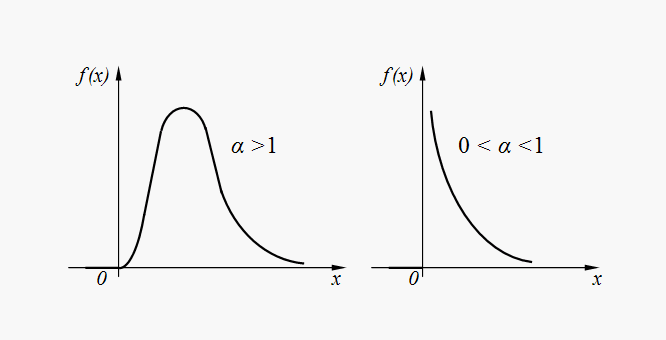Распределения непрерывных случайных величинРавномерное распределение. Непрерывная величина Х распределена равномерно на интервале ( a , b ), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:
Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда
Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение , если плотность распределения ее вероятностей выражается формулой:
График плотности распределения вероятностей (31) представлен на рис. 5.
Время
Т
безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром
λ
, физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.
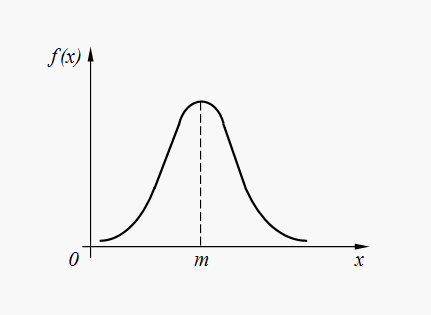
Нормальное (гауссово) распределение. Случайная величина Х имеет нормальное (гауссово) распределение , если плотность распределения ее вероятностей определяется зависимостью:
где
m
=
M
(
X
) ,
При
График плотности нормального распределения (32) представлен на рис. 6.
Нормальное распределение является наиболее часто встречающимся в различных случайных явлениях природы. Так, ошибки выполнения команд автоматизированным устройством, ошибки вывода космического корабля в заданную точку пространства, ошибки параметров компьютерных систем и т.д. в большинстве случаев имеют нормальное или близкое к нормальному распределение. Более того, случайные величины, образованные суммированием большого количества случайных слагаемых, распределены практически по нормальному закону.
Гамма-распределение. Случайная величина Х имеет гамма-распределение , если плотность распределения ее вероятностей выражается формулой:
где
Основные свойства гамма-функции:
Параметры
|
Содержание
>> Прикладная математика
>> Математическая статистика
>> Элементы математической статистики
>> Распределения непрерывных случайных величин
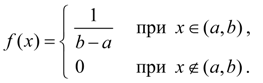 (29)
(29)
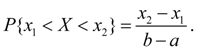 (30)
(30)
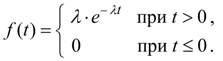 (31)
(31)
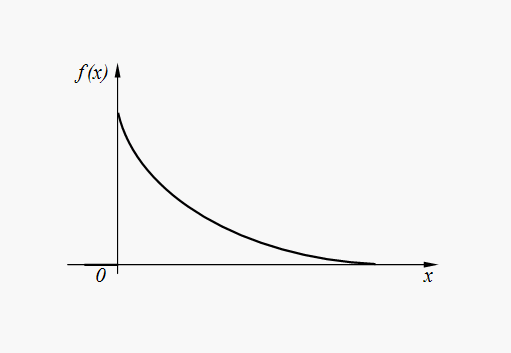
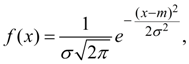 (32)
(32)
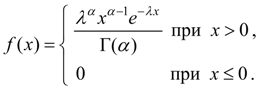 (33)
(33)
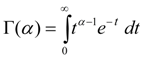 – гамма-функция Эйлера.
– гамма-функция Эйлера.