Числовые характеристики случайных величинМатематическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f ( x ):
Несобственный интеграл (6 б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М ( Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины. Свойства математического ожидания:
Дисперсия. Дисперсией случайной величины Х называется число:
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
Здесь m = М ( Х ). Свойства дисперсии:
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М ( Х – х 0 ) k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение
С
ее центр распределения сдвигается на то же значение
С
, а отклонение от центра не меняется:
Х
–
m
= (
Х
–
С
) – (
m
–
С
).
Асимметрия. Центральный момент третьего порядка:
служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :
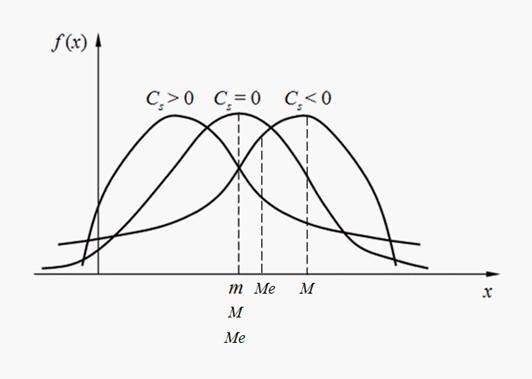
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).
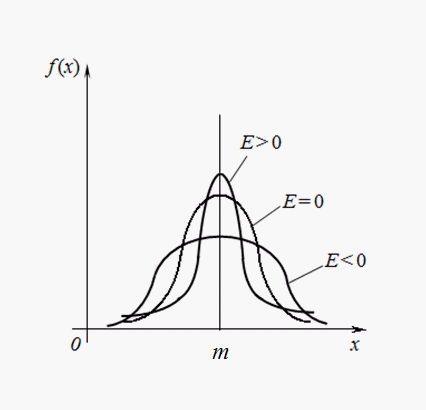
Эксцесс. Центральный момент четвертого порядка:
служит для оценки так называемого
эксцесса
, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода
дискретной
случайной величины – это ее наиболее вероятное значение.
Модой
непрерывной
случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется
унимодальным
. Если кривая распределения имеет более одного максимума, то распределение называется
полимодальным
. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются
антимодальными
. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для
модального
, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана
случайной величины
Х
– это ее значение
Ме
, для которого имеет место равенство:
|
Содержание
>> Прикладная математика
>> Математическая статистика
>> Элементы математической статистики
>> Числовые характеристики случайных величин
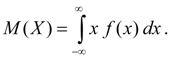 (6
б
)
(6
б
)
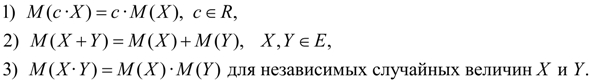 (7)
(7)
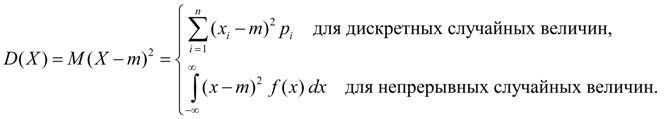 (9)
(9)
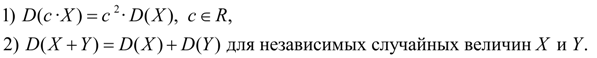 (10)
(10)
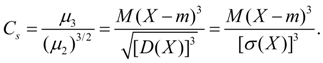 (18)
(18)
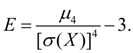 (20)
(20)