Динамический синтез - Планирование закона торможения поршня гидроцилиндра
Планирование закона торможения поршня гидроцилиндра
Математическая модель рассматриваемой системы имеет вид:
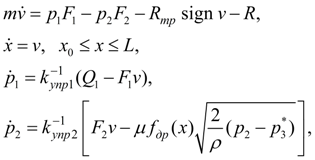 (1)
(1)
где
т
– приведенная к штоку гидроцилиндра масса подвижных частей;
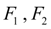 – площади напорной и сливной полостей гидроцилиндра;
– площади напорной и сливной полостей гидроцилиндра;
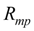 – сила сухого трения в манжетных уплотнениях, равная
– сила сухого трения в манжетных уплотнениях, равная
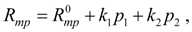
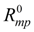 – сила сухого трения при отсутствии давления;
– сила сухого трения при отсутствии давления;
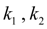 – коэффициенты пропорциональности;
R
– внешняя сила на штоке;
– коэффициенты пропорциональности;
R
– внешняя сила на штоке;
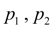 – давления в напорной и сливной полостях гидроцилиндра;
– давления в напорной и сливной полостях гидроцилиндра;
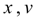 – перемещение и скорость поршня;
– перемещение и скорость поршня;
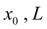 – начальное положение и полный ход поршня;
– начальное положение и полный ход поршня;
 – коэффициенты упругости жидкости в полостях гидроцилиндра, равные:
– коэффициенты упругости жидкости в полостях гидроцилиндра, равные:
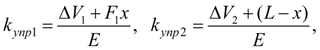
Е
– приведенный объемный модуль упругости рабочей жидкости в упругой оболочке:
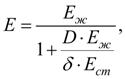
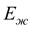 – объемный модуль упругости рабочей жидкости;
– объемный модуль упругости рабочей жидкости;
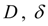 – диаметр и толщина стенки цилиндра;
– диаметр и толщина стенки цилиндра;
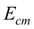 – модуль упругости материала стенки цилиндра;
– модуль упругости материала стенки цилиндра;
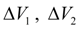 – «мертвые» объемы полостей цилиндра;
– «мертвые» объемы полостей цилиндра;
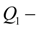 расход рабочей жидкости в напорную полость цилиндра;
расход рабочей жидкости в напорную полость цилиндра;
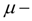 коэффициент расхода дросселя;
коэффициент расхода дросселя;
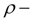 плотность рабочей жидкости;
плотность рабочей жидкости;
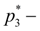 давление на сливе за дросселем;
давление на сливе за дросселем;
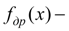 площадь проходного сечения дросселя в функции перемещения поршня.
площадь проходного сечения дросселя в функции перемещения поршня.
Проведенные по модели (1) динамические расчеты переходных процессов, возникающих при торможении в ряде гидроцилиндров с учетом их геометрии, расчетной семы нагрузок (препятствующих или попутных), различных форм дросселирующих щелей, приведенных масс и т.д., носившие поверочный характер, показали, что выбор той или иной зависимости
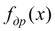 оказывает существенное влияние на динамику тормозных процессов в гидроцилиндре и поэтому должен быть согласован как с параметрами гидропривода (приведенные к штоку масса и нагрузка, упругость гидросистемы и т.д.), так и с заданными к процессу торможения требованиями (время и ход торможения, пиковые давления и т.д.)
оказывает существенное влияние на динамику тормозных процессов в гидроцилиндре и поэтому должен быть согласован как с параметрами гидропривода (приведенные к штоку масса и нагрузка, упругость гидросистемы и т.д.), так и с заданными к процессу торможения требованиями (время и ход торможения, пиковые давления и т.д.)
Для решения поставленной задачи примем ряд допущений:
1) до начала торможения скорость поршня, давления в полостях гидроцилиндра и расход рабочей жидкости постоянны;
2) учитывая, что торможение поршня происходит на относительно малом перемещении, можно считать приведенные массу и силу на штоке гидроцилиндра постоянными;
3) целесообразно задать такой закон движения поршня при торможении, при котором скорость
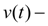 строго убывающая функция, что позволяет принять
строго убывающая функция, что позволяет принять
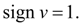
Исходя из этого, спланируем закон движения поршня
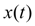 в период торможения
в период торможения
 , приняв следующие граничные условия:
, приняв следующие граничные условия:
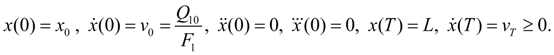 (2)
(2)
Здесь
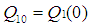 ,
,
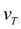 – конечная скорость поршня;
Т
– время торможения.
– конечная скорость поршня;
Т
– время торможения.
Наложим ограничение на максимальное давление
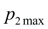 :
:
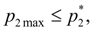 (3)
(3)
откуда с учетом (1) следует:
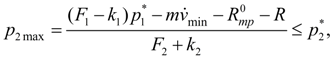 (4)
(4)
где
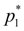 – давление настройки предохранительного клапана гидросистемы. Считаем, что расход на входе в гидроцилиндр изменяется в соответствии со статической характеристикой клапана:
– давление настройки предохранительного клапана гидросистемы. Считаем, что расход на входе в гидроцилиндр изменяется в соответствии со статической характеристикой клапана:
 (5)
(5)
Здесь
 – разность давлений настройки и срабатывания предохранительного клапана.
– разность давлений настройки и срабатывания предохранительного клапана.
Из (4) следует:
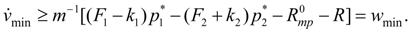 (6)
(6)
Отметим, что задавая максимально допустимое давление
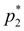 , необходимо обеспечить выполнение условия
, необходимо обеспечить выполнение условия
 поскольку иначе торможение поршня невозможно.
поскольку иначе торможение поршня невозможно.
Исключив
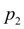 из уравнений (1), получим:
из уравнений (1), получим:
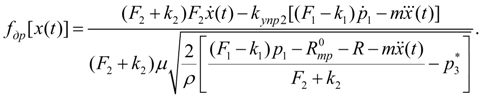 (7)
(7)
При заданном законе движения поршня величины
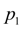 и
и
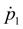 , входящие в формулу (7), могут быть определены либо путем численного интегрирования третьего уравнения системы (1), либо аналитически, поскольку уравнение относительно
, входящие в формулу (7), могут быть определены либо путем численного интегрирования третьего уравнения системы (1), либо аналитически, поскольку уравнение относительно
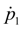 является практически кусочно-линейным
является практически кусочно-линейным
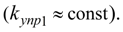 В его правой части содержится известная функция
В его правой части содержится известная функция
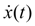 , а расход
, а расход
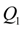 описывается кусочно-линейной зависимостью (5). Любой из этих способов обеспечивает получение искомой зависимости
описывается кусочно-линейной зависимостью (5). Любой из этих способов обеспечивает получение искомой зависимости
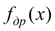 в параметрической форме:
в параметрической форме:
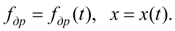 (8)
(8)
Имея
шесть
граничных условий (2), спланируем закон движения поршня с помощью полинома
пятой
степени:
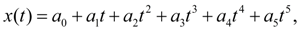 (9)
(9)
Откуда, дифференцируя, получим
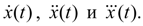
Используя граничные условия (2), приходим к системе линейных алгебраических уравнений относительно неизвестных коэффициентов
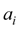 полинома (9), решение которой:
полинома (9), решение которой:
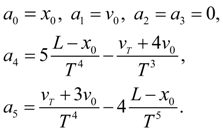 (10)
(10)
Поскольку начальное положение поршня
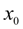 заранее неизвестно, то для его определения, не повышая степени полинома (9), наложим дополнительное граничное условие:
заранее неизвестно, то для его определения, не повышая степени полинома (9), наложим дополнительное граничное условие:
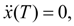 (11)
(11)
которое с учетом (9) и (10) дает:
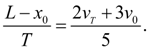 (12)
(12)
Тогда
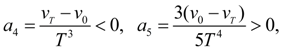 (13)
(13)
откуда следует, что при
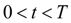 имеет место
имеет место
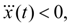 т.е. обеспечивается требуемая монотонность
т.е. обеспечивается требуемая монотонность
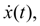 а
а
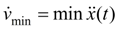 достигается при
достигается при
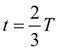 и равен:
и равен:
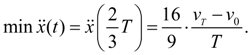 (14)
(14)
Тогда из (6) следует:
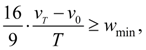 (15)
(15)
откуда окончательно
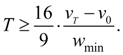 (16)
(16)
Следовательно, задав время торможения
Т
из условия (16) и используя (12), получим
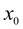 .
.
|
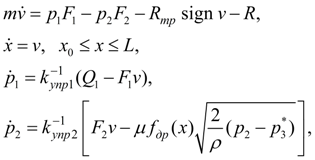 (1)
(1)
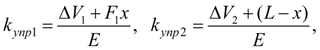
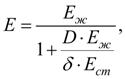
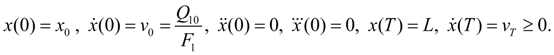 (2)
(2)
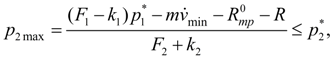 (4)
(4)
 (5)
(5)
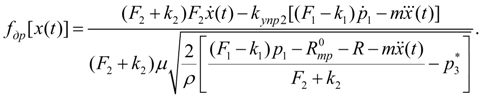 (7)
(7)
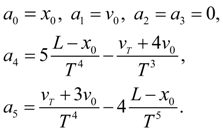 (10)
(10)
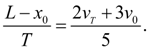 (12)
(12)
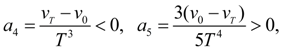 (13)
(13)
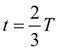 и равен:
и равен:
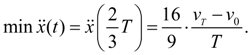 (14)
(14)
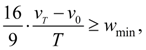 (15)
(15)
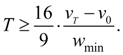 (16)
(16)